2-3 Inequalities among Logical and Arithmetic Expressions

Inequalities among binary logical expressions whose values are interpreted as unsigned integers are nearly trivial to derive. Here are two examples:

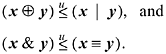
These can be derived from a list of all binary logical operations, shown in Table 2-1.

Let f(x, y) and g(x, y) represent two columns in Table 2-1. If for each row in which f(x, y) is 1, g(x, y) also is 1, then for all (x, y), Clearly, this extends to word-parallel logical operations. One can easily read off such relations (most of which are trivial) as and so on. Furthermore, if two columns have a row in which one entry is 0 and the other is 1, and another row in which the entries are 1 and 0, respectively, then no inequality relation exists between the corresponding logical expressions. So the question of whether or not is completely and easily solved for all binary logical functions f and g.

Table 2-1. The 16 Binary Logical Operations
x	y	0	x & y	x & ?span class=docemphasis1>y	x	?span class=docemphasis1>x & y	y	x y	x | y	?x | y)	x y	?span class=docemphasis1>y	x | ?span class=docemphasis1>y	?span class=docemphasis1>x	?span class=docemphasis1>x | y	?x & y)	1
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

Use caution when manipulating these relations. For example, for ordinary arithmetic, if x + y a and z x, then z + y a. But this inference is not valid if "+" is replaced with or.

Inequalities involving mixed logical and arithmetic expressions are more interesting. Below is a small selection.

a.

b.

c.

d.

e.

The proofs of these are quite simple, except possibly for the relation By |x - y| we mean the absolute value of x - y, which may be computed within the domain of unsigned numbers as max(x, y) - min(x, y). This relation may be proven by induction on the length of x and y (the proof is a little easier if you extend them on the left rather than on the right).