2-8 Three-Valued Compare Function

The three-valued compare function, a slight generalization of the sign function, is defined by

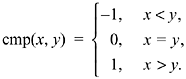
There are both signed and unsigned versions, and unless otherwise specified, this section applies to both.

Comparison predicate instructions permit a three-instruction solution, an obvious generalization of Equations (3):

A solution for unsigned integers on PowerPC is shown below [CWG]. On this machine, "carry" is "not borrow."

subf?R5,Ry,Rx   # R5 <-- Rx - Ry. 
subfc R6,Rx,Ry   # R6 <-- Ry - Rx, set carry. 
subfe R7,Ry,Rx   # R7 <-- Rx - Ry + carry, set carry. 
subfe R8,R7,R5   # R8 <-- R5 - R7 + carry, (set carry). 

If limited to the instructions of the basic RISC, there does not seem to be any particularly good way to compute this function. The comparison predicates x < y, x y, and so on, require about five instructions (see Section 2-11), leading to a solution in about 12 instructions (using a small amount of commonality in computing x < y and x > y). On the basic RISC it's probably preferable to use compares and branches (six instructions executed worst case if compares can be commoned).