8-1 Multiword Multiplication

This may be done with, basically, the traditional grade-school method. Rather than develop an array of partial products, however, it is more efficient to add each new row, as it is being computed, into a row that will become the product.

If the multiplicand is m words, and the multiplier is n words, then the product occupies m + n words (or fewer), whether signed or unsigned.

In applying the grade-school scheme, we would like to treat each 32-bit word as a single digit. This works out well if an instruction that gives the 64-bit product of two 32-bit integers is available. Unfortunately, even if the machine has such an instruction, it is not readily accessible from most high-level languages. In fact, many modern RISC machines do not have this instruction in part because it isn't accessible from high-level languages and thus would not often be used. (Another reason is that the instruction would be one of a very few that give a two-register result.)

Our procedure is shown in Figure 8-1. It uses halfwords as the "digits." Parameter w gets the result, and u and v are the multiplier and multiplicand, respectively. Each is an array of halfwords, with the first halfword (w[0], u[0], and v[0]) being the least significant digit. This is "little-endian" order. Parameters m and n are the number of halfwords in u and v, respectively.

The picture below may help in understanding. There is no relation between m and n; either may be the larger.

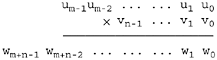
The procedure follows Algorithm M of [Knu2, sec. 4.3.1], but is coded in C and modified to perform signed multiplication. Observe that the assignment to t in the upper half of Figure 8-1 cannot overflow, because the maximum value that could be assigned to t is (2¹⁶ - 1)² + 2(2¹⁶ - 1) = 2³² - 1.

Multiword multiplication is simplest for unsigned operands. In fact, the code of Figure 8-1 performs unsigned multiplication if the "correction" steps (the lines between the three-line comment and the "return" statement) are omitted. An unsigned version can be extended to signed in three ways:

Figure 8-1 Multiword integer multiplication, signed.

void mulmns(unsigned short w[], unsigned short u[], 
   unsigned short v[], int m, int n) {
   unsigned int k, t, b; 
   int i, j; 
 
   for (i = 0; i < m; i++) 
      w[i] = 0; 
 
   for (j = 0; j < n; j++) {
    ?k = 0; 
      for (i = 0; i < m; i++) {
         t = u[i]*v[j] + w[i + j] + k; 
         w[i + j] = t;        ?// (I.e., t & 0xFFFF). 
         k = t >> 16; 
      } 
      w[j + m] = k; 
   } 
 
   // Now w[] has the unsigned product. Correct by 
  ?/ subtracting v*2**16m if u < 0, and 
  ?/ subtracting u*2**16n if v < 0. 
 
   if ((short)u[m - 1] < 0) {
    ?b = 0;                  ?// Initialize borrow. 
      for (j = 0; j < n; j++) {
         t = w[j + m] - v[j] - b; 
         w[j + m] = t; 
         b = t >> 31; 
      } 
   } 
   if ((short)v[n - 1] < 0) {
    ?b = 0; 
      for (i = 0; i < m; i++) {
         t = w[i + n] - u[i] - b; 
         w[i + n] = t; 
         b = t >> 31; 
      } 
   } 
   return; 
} 

1. Take the absolute value of each input operand, perform unsigned multiplication, and then negate the result if the input operands had different signs.

2. Perform the multiplication using unsigned elementary multiplication except when multiplying one of the high-order halfwords, in which case use signed x unsigned or signed x signed multiplication.

3. Perform unsigned multiplication and then correct the result somehow.

The first method requires passing over as many as m + n input halfwords, to compute their absolute value. Or, if one operand is positive and one is negative, the method requires passing over as many as max(m, n) + m + n halfwords, to complement the negative input operand and the result. Perhaps more serious, the algorithm would alter its inputs (which we assume are passed by address), which may be unacceptable in some applications. Alternatively, it could allocate temporary space for them, or it could alter them and later change them back. All these alternatives are unappealing.

The second method requires three kinds of elementary multiplication (unsigned x unsigned, unsigned x signed, and signed x signed) and requires sign extension of partial products on the left, with 0's or 1's, making each partial product take longer to compute and add to the running total.

We choose the third method. To see how it works, let u and v denote the values of the two signed integers being multiplied, and let them be of lengths M and N bits, respectively. Then the steps in the upper half of Figure 8-1 erroneously interpret u as an unsigned quantity, having value u + 2^Mu_{M - 1}, where u_{M - 1} is the sign bit of u. That is, u_{M - 1} = 1 if u is negative, and u_{M - 1} = 0 otherwise. Similarly, the program interprets v as having value v + 2^Nu_{N - 1}.

The program computes the product of these unsigned numbers—that is, it computes

To get the desired result (uv), we must subtract from the unsigned product the value 2^Mu_{M - 1} v + 2^Nv_{N - 1} u. There is no need to subtract the term 2^{M + N}u_{M - 1} v_{N - 1}, because we know that the result can be expressed in M + N bits, so there is no need to compute any product bits more significant than bit position M + N - 1. These two subtractions are performed by the steps below the three-line comment in Figure 8-1. They require passing over a maximum of m + n halfwords.

It might be tempting to use the program of Figure 8-1 by passing it an array of fullword integers—that is, by "lying across the interface." Such a program will work on a little-endian machine, but not on a big-endian one. If we had stored the arrays in the reverse order, with u[0] being the most significant halfword (and the program altered accordingly), the "lying" program would work on a big-endian machine, but not on a little-endian one.