10-4 Signed Division by Divisors 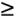2

At this point you may wonder if other divisors present other problems. We see in this section that they do not; the three examples given illustrate the only cases that arise (for d 2).

Some of the proofs are a bit complicated, so to be cautious, the work is done in terms of a general word size W.

Given a word size W 3 and a divisor d, 2 d < 2^{W - 1}, we wish to find the least integer m and integer p such that

Equation 1a

 

Equation 1b

 

with 0 m < 2^W and p W.

The reason we want the least integer m is that a smaller multiplier may give a smaller shift amount (possibly zero) or may yield code similar to the "divide by 5" example, rather than the "divide by 7" example. We must have m 2^{W - 1} so the code has no more instructions than that of the "divide by 7" example (that is, we can handle a multiplier in the range 2^{W - 1} to 2^{W - 1} by means of the add that was inserted in the "divide by 7" example, but we would rather not deal with larger multipliers). We must have p W because the generated code extracts the left half of the product mn, which is equivalent to shifting right W positions. Thus, the total right shift is W or more positions.

There is a distinction between the multiplier m and the "magic number," denoted M. The magic number is the value used in the multiply instruction. It is given by

 

Because (1b) must hold for which implies

Equation 2

 

Let n_c be the largest (positive) value of n such that (n_c, d) = d - 1. n_c exists because one possibility is n_c = d - 1. It can be calculated from n_c is one of the highest d admissible values of n, so

Equation 3a

 

and clearly

Equation 3b

 

Because (1a) must hold for n = n_c,

 

or

 

Combining this with (2) gives

Equation 4

 

Because m is to be the least integer satisfying (4), it is the next integer greater than 2^p/d; that is,

Equation 5

 

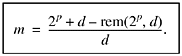
Combining this with the right half of (4) and simplifying gives

Equation 6

 

The Algorithm

Thus, the algorithm to find the magic number M and the shift amount s from d is to first compute n_c, and then solve (6) for p by trying successively larger values. If p < W, set p = W (the theorem below shows that this value of p also satisfies (6)). When the smallest p W satisfying (6) is found, m is calculated from (5). This is the smallest possible value of m, because we found the smallest acceptable p, and from (4) clearly smaller values of p yield smaller values of m. Finally, s = p - W and M is simply a reinterpretation of m as a signed integer (which is how the mulhs instruction interprets it).

Forcing p to be at least W is justified by the following:

Theorem DC1. If (6) is true for some value of p, then it is true for all larger values of p.

Proof. Suppose (6) is true for p = p₀. Multiplying (6) by 2 gives

 

From Theorem D5, Combining gives

 

Therefore, (6) is true for p = p₀ + 1, and hence for all larger values.

Thus, one could solve (6) by a binary search, although a simple linear search (starting with p = W) is probably preferable, because usually d is small, and small values of d give small values of p.

Proof That the Algorithm Is Feasible

We must show that (6) always has a solution and that 0 m < 2^W. (It is not necessary to show that p W, because that is forced.)

We show that (6) always has a solution by getting an upper bound on p. As a matter of general interest, we also derive a lower bound under the assumption that p is not forced to be at least W. To get these bounds on p, observe that for any positive integer x, there is a power of 2 greater than x and less than or equal to 2x. Hence from (6),

 

Because 0 rem(2^p, d) d - 1,

Equation 7

 

From (3a) and (3b), n_c max(2^{W - 1} - d, d - 1). The lines f₁(d) = 2^{W - 1} - d and f₂(d) = d - 1 cross at d = (2^{W - 1} + 1)/2. Hence n_c (2^{W - 1} - 1)/2. Because n_c is an integer, n_c 2^{W - 2}. Because n_c, d 2^{W - 1} - 1, (7) becomes

 

or

Equation 8

 

The lower bound p = W - 1 can occur (e.g., for W = 32, d = 3), but in that case we set p = W.

If p is not forced to equal W, then from (4) and (7),

 

Using (3b) gives

 

Because n_c 2^{W - 1} - 1(3a),

 

If p is forced to equal W, then from (4),

 

Because 2 d 2^{W - 1} - 1 and n_c 2^{W - 2},

 

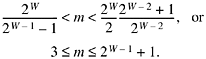
Hence in either case m is within limits for the code schema illustrated by the "divide by 7" example.

Proof That the Product Is Correct

We must show that if p and m are calculated from (6) and (5), then equations (1a) and (1b) are satisfied.

Equation (5) and inequality (6) are easily seen to imply (4). (In the case that p is forced to be equal to W, (6) still holds, as shown by Theorem DC1.) In what follows, we consider separately the following five ranges of values of n:

 

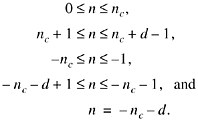
From (4), because m is an integer,

 

Multiplying by n/2^p, for n 0 this becomes

 

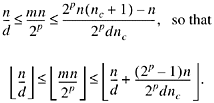
For 0 n n_c, 0 (2^p - 1)n/(2^pdn_c) < 1/d, so by Theorem D4,

 

Hence (1a) is satisfied in this case (0 n n_c).

For n > n_c, n is limited to the range

Equation 9

 

because n n_c + d contradicts the choice of n_c as the largest value of n such that rem(n_c, d) = d - 1 (alternatively, from (3a), n n_c + d implies n 2^{W - 1}). From (4), for n 0,

 

By elementary algebra, this can be written

Equation 10

 

From (9), 1 n - n_c d - 1, so

 

Because n_c d - 1 (by (3b)) and (n_c + 1)/n_c has its maximum when n_c has its minimum,

 

In (10), the term (n_c + 1)/d is an integer. The term (n - n_c)(n_c + 1)/dn_c is less than or equal to 1. Therefore, (10) becomes

 

For all n in the range (9), Hence (1a) is satisfied in this case (n_c + 1 n n_c + d - 1).

For n < 0, from (4) we have, because m is an integer,

 

Multiplying by n/2^p for n < 0 this becomes

 

or

 

Using Theorem D2 gives

 

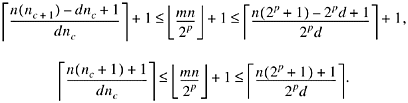
Because n + 1 0, the right inequality can be weakened, giving

Equation 11

 

For -n_c n - 1,

 

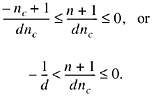
Hence by Theorem D4,

 

so that (1b) is satisfied in this case (-n_c n -1).

For n < -n_c, n is limited to the range

Equation 12

 

(From (3a), n < - n_c - d implies that n < -2^{W - 1}, which is impossible.) Performing elementary algebraic manipulation of the left comparand of (11) gives

Equation 13

 

For -n_c - d n - n_c - 1,

 

The ratio (n_c + 1)/n_c is a maximum when n_c is a minimum; that is, n_c = d - 1. Therefore,

 

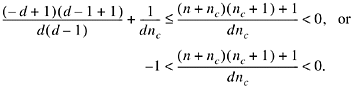
From (13), because (- n_c - 1)/d is an integer and the quantity added to it is between 0 and -1,

 

For n in the range - n_c - d + 1 n - n_c - 1,

 

Hence —that is, (1b) is satisfied.

The last case, n = - n_c - d, can occur only for certain values of d. From (3a), - n_c - d - 2^{W - 1}, so if n takes on this value, we must have n = -n_c - d = -2^{W - 1}, and hence n_c = 2^{W - 1} - d. Therefore, rem(2^{W - 1}, d)= rem(n_c + d, d) = d - 1 (that is, d divides 2^{W - 1} + 1).

For this case (n = - n_c - d), (6) has the solution p = W - 1(the smallest possible value of p), because for p = W - 1,

 

Then from (5),

 

Therefore,

 

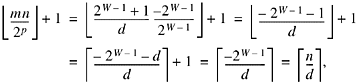
so that (1b) is satisfied.

This completes the proof that if m and p are calculated from (5) and (6), then Equations (1a) and (1b) hold for all admissible values of n.