10-7 Miscellaneous Topics

Theorem DC2. The least multiplier m is odd if p is not forced to equal W.

Proof. Assume that Equations (1a) and (1b) are satisfied with least (not forced) integer p, and m even. Then clearly m could be divided by 2 and p could be decreased by 1, and (1a) and (1b) would still be satisfied. This contradicts the assumption that p is minimal.

Uniqueness

The magic number for a given divisor is sometimes unique (e.g., for W = 32, d = 7), but often it is not. In fact, experimentation indicates that it is usually not unique. For example, for W = 32, d = 6, there are four magic numbers:

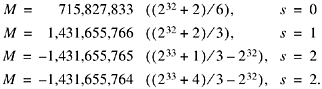
However, there is the following uniqueness property:

Theorem DC3. For a given divisor d, there is only one multiplier m having the minimal value of p, if p is not forced to equal W.

Proof. First consider the case d > 0. The difference between the upper and lower limits of inequality (4) is 2^p/dn_c. We have already proved (7) that if p is minimal, then 2^p/dn_c 2. Therefore, there can be at most two values of m satisfying (4). Let m be the smaller of these values, given by (5); then m + 1 is the other.

Let p₀ be the least value of p for which m + 1 satisfies the right half of (4) (p₀ is not forced to equal W). Then

This simplifies to

Dividing by 2 gives

Because (by Theorem D5 on page 140),

contradicting the assumption that p₀ is minimal.

The proof for d < 0 is similar and will not be given.

The Divisors with the Best Programs

The program for d = 3, W = 32 is particularly short, because there is no add or shrsi after the mulhs. What other divisors have this short program?

We consider only positive divisors. We wish to find integers m and p that satisfy equations (1a) and (1b), and for which p = W and 0 m 2^{W - 1}. Because any integers m and p that satisfy equations (1a) and (1b) must also satisfy (4), it suffices to find those divisors d for which (4) has a solution with p = W and 0 m < 2^{W - 1}. All solutions of (4) with p = W are given by

Combining this with the right half of (4) and simplifying gives

Equation 21

The weakest restriction on rem(2^W, d) is with k = 1 and n_c at its minimal value of 2^{W - 2}. Hence we must have

that is, d divides 2^W + 1, 2^W + 2, or 2^W + 3.

Now let us see which of these factors actually have optimal programs.

If d divides 2^W + 1, then rem(2^W, d) = d - 1. Then a solution of (6) is p = W, because the inequality becomes

which is obviously true, because n_c < 2^{W - 1}. Then in the calculation of m we have

which is less than 2^{W - 1} for d 3 (d 2 because d divides 2^W + 1). Hence all the factors of 2^W + 1 have optimal programs.

Similarly, if d divides 2^W + 2, then rem(2^W, d) = d - 2. Again, a solution of (6) is p = W, because the inequality becomes

which is obviously true. Then in the calculation of m we have

which exceeds 2^{W - 1} - 1 for d = 2, but which is less than or equal to 2^{W - 1} - 1 for W 3, d 3 (the case W = 3 and d = 3 does not occur, because 3 is not a factor of 2³ + 2 = 10). Hence all factors of 2^W + 2, except for 2 and the cofactor of 2, have optimal programs. (The cofactor of 2 is (2^W + 2)/2, which is not representable as a W-bit signed integer).

If d divides 2^W + 3, the following argument shows that d does not have an optimal program. Because rem(2^W, d) = d - 3, inequality (21) implies that we must have

for some k = 1, 2, 3, ? The weakest restriction is with k = 1, so we must have n_c < 2^W/3.

From (3a), n_c 2^{W - 1} - d, or d 2^{W - 1} - n_c. Hence it is necessary that

Also, since 2, 3, and 4 do not divide 2^W + 3, the smallest possible factor of 2^W + 3 is 5. Hence the largest possible factor is (2^W + 3)/5. Thus, if d divides 2^W + 3 and d has an optimal program, it is necessary that

Taking reciprocals of this with respect to 2^W + 3 shows that the cofactor of d, (2^W + 3)/d, has the limits

For W 5, this implies that the only possible cofactors are 5 and 6. For W < 5, it is easily verified that there are no factors of 2^W + 3. Because 6 cannot be a factor of 2^W + 3, the only possibility is 5. Therefore, the only possible factor of 2^W + 3 that might have an optimal program is (2^W + 3)/5.

For d = (2^W + 3)/5,

For W 4,

so

This exceeds (2^W/3), so d = (2^W + 3)/5 does not have an optimal program. Because for W < 4 there are no factors of 2^W + 3, we conclude that no factors of 2^W + 3 have optimal programs.

In summary, all the factors of 2^W + 1 and of 2^W + 2, except for 2 and (2^W + 2)/2, have optimal programs, and no other numbers do. Furthermore, the above proof shows that algorithm magic (Figure 10-1 on page 174) always produces the optimal program when it exists.

Let us consider the specific cases W = 16, 32, and 64. The relevant factorizations are shown below.

Hence we have the results that for W = 16, there are 20 divisors that have optimal programs. The ones less than 100 are 3, 6, 9, 11, 18, 22, 33, 66, and 99.

For W = 32, there are six such divisors: 3, 6, 641, 6,700,417, 715,827,883, and 1,431,655,766.

For W = 32, there are 126 such divisors. The ones less than 100 are 3, 6, 9, 18, 19, 27, 38, 43, 54, 57, and 86.