10-9 Unsigned Division by Divisors 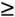1

Given a word size W 1 and a divisor d, 1 d < 2^W, we wish to find the least integer m and integer p such that

Equation 22

with 0 m < 2^{W + 1} and p W.

In the unsigned case, the magic number M is given by

Because (22) must hold for

Equation 23

As in the signed case, let n_c be the largest value of n such that rem(n_c, d) = d - 1. It can be calculated from Then

Equation 24a

and

Equation 24b

These imply that n_c 2^{W - 1}.

Because (22) must hold for n = n_c,

or

Combining this with (23) gives

Equation 25

Because m is to be the least integer satisfying (25), it is the next integer greater than or equal to 2^p/d—that is,

Equation 26

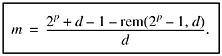
Combining this with the right half of (25) and simplifying gives

Equation 27

The Algorithm (Unsigned)

Thus, the algorithm is to find by trial and error the least p W satisfying (27). Then m is calculated from (26). This is the smallest possible value of m satisfying (22) with p W. As in the signed case, if (27) is true for some value of p, then it is true for all larger values of p. The proof is essentially the same as that of Theorem DC1, except Theorem D5(b) is used instead of Theorem D5(a).

Proof That the Algorithm Is Feasible (Unsigned)

We must show that (27) always has a solution and that 0 m < 2^{W + 1}.

Because for any nonnegative integer x there is a power of 2 greater than x and less than or equal to 2x + 1, from (27),

Because 0 rem(2^{p - 1}, d) d - 1,

Equation 28

Because n_c, d 2^{W - 1}, this becomes

or

Equation 29

Thus, (27) always has a solution.

If p is not forced to equal W, then from (25) and (28),

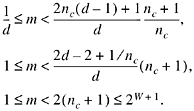
If p is forced to equal W, then from (25),

Because 1 d 2^W - 1 and n_c 2^{W - 1},

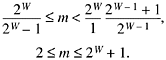
Hence in either case m is within limits for the code schema illustrated by the "unsigned divide by 7" example.

Proof That the Product Is Correct (Unsigned)

We must show that if p and m are calculated from (27) and (26), then (22) is satisfied.

Equation (26) and inequality (27) are easily seen to imply (25). Inequality (25) is nearly the same as (4), and the remainder of the proof is nearly identical to that for signed division with n 0.