11-4 Integer Logarithm

By the "integer logarithm" function we mean the function where x is a positive integer and b is an integer greater than or equal to 2. Usually, b = 2 or 10, and we denote these functions by "ilog2" and "ilog10," respectively. We use "ilog" when the base is unspecified.

It is convenient to extend the definition to x = 0 by defining ilog(0) = -1 [CJS]. There are several reasons for this definition:

?span style='font:7.0pt "Times New Roman"'>         The function ilog2(x) is then related very simply to the number of leading zeros function, nlz(x), by the formula shown below, including the case x = 0. Thus, if one of these functions is implemented in hardware or software, the other is easily obtained.

?span style='font:7.0pt "Times New Roman"'>         It is easy to compute using the formula below. For x = 1, this formula implies that ilog(0) = -1.

?span style='font:7.0pt "Times New Roman"'>         It makes the following identity hold for x = 1 (but it doesn't hold for x = 0):

?span style='font:7.0pt "Times New Roman"'>         It preserves the mathematical identity:

?span style='font:7.0pt "Times New Roman"'>         It makes the result of ilog(x) a small dense set of integers (-1 to 31 for ilog2(x) on a 32-bit machine, with x unsigned), making it directly useful for indexing a table.

?span style='font:7.0pt "Times New Roman"'>         It falls naturally out of several algorithms for computing ilog2(x) and ilog10(x).

Unfortunately, it isn't the right definition for "number of digits of x," which is ilog(x) + 1 for all x except x = 0. But it seems best to consider that anomalous.

For x < 0, ilog(x) is left undefined. To extend its range of utility, we define the function as mapping unsigned numbers to signed numbers. Thus, a negative argument cannot occur.

Integer Log Base 2

Computing ilog2(x) is essentially the same as computing the number of leading zeros, which is discussed in "Counting Leading 0's" on page 77. All the algorithms in that section can be easily modified to compute ilog2(x) directly, rather than by computing nlz(x) and subtracting the result from 31. (For the algorithm of Figure 5-11 on page 80, change the line return pop(~x) to return pop(x) - 1).

Integer Log Base 10

This function has application in converting a number to decimal for inclusion into a line with leading zeros suppressed. The conversion process successively divides by 10, producing the least significant digit first. It would be useful to know ahead of time where the least significant digit should be placed, to avoid putting the converted number in a temporary area and then moving it.

To compute ilog10(x), a table search is quite reasonable. This could be a binary search, but because the table is small and in many applications x is usually small, a simple linear search is probably best. This rather straightforward program is shown in Figure 11-7.

Figure 11-7 Integer log base 10, simple table search.

int ilog10(unsigned x) {
   int i; 
  ?span
lang=EN-GB>static unsigned table[11] = {0, 9, 99, 999, 9999, 
      99999, 999999, 9999999, 99999999, 999999999, 
      0xFFFFFFFF}; 
 
   for (i = -1; ; i++) {
      if (x <= table[i+1]) return i; 
   } 
} 

On the basic RISC, this program can be implemented to execute in about instructions. Thus, it executes in five to 45 instructions, with perhaps 13 (for 10 x 99) being typical.

The program in Figure 11-7 can easily be changed into an "in register" version (not using a table). The executable part of such a program is shown in Figure 11-8. This might be useful if the machine has a fast way to multiply by 10.

Figure 11-8 Integer log base 10, repeated multiplication by 10.

p = 1; 
for (i = -1; i <= 8; i++) {
   if (x < p) return i; 
   p = 10*p; 
} 
return i; 

This program can be implemented to execute in about instructions on the basic RISC (counting the multiply as one instruction). This amounts to 16 instructions for 10 x 99.

A binary search can be used, giving an algorithm that is loop-free and does not use a table. Such an algorithm might compare x to 10⁴, then to either 10² or to 10⁶, and so on, until the exponent n is found such that 10ⁿ x < 10^{n + 1}. The paths execute in ten to 18 instructions, four or five of which are branches (counting the final unconditional branch).

The program shown in Figure 11-9 is a modification of the binary search that has a maximum of four branches on any path, and is written in a way that favors small x. It executes in six basic RISC instructions for 10 x 99, and in 11 to 16 instructions for x 100.

Figure 11-9 Integer log base 10, modified binary search.

int ilog10(unsigned x) {
   if (x > 99) 
      if (x < 1000000) 
         if (x < 10000) 
            return 3 + ((int)(x - 1000) >> 31); 
         else 
            return 5 + ((int)(x - 100000) >> 31); 
      else 
         if (x < 100000000) 
            return 7 + ((int)(x - 10000000) >> 31); 
         else 
            return 9 + ((int)((x-1000000000)&~x) >> 31); 
   else 
      if (x > 9) return 1; 
      else       return ((int)(x - 1) >> 31); 
} 

The shift instructions in this program are signed shifts (which is the reason for the (int) casts). If your machine does not have this instruction, one of the alternatives below, which use unsigned shifts, may be preferable. These are illustrated for the case of the first return statement. Unfortunately, the first two require subtract from immediate for efficient implementation, which most machines don't have. The last involves adding a large constant (two instructions), but this does not matter for the second and third return statements, which require adding a large constant anyway. The large constant is 2³¹ - 1000.

return 3 - ((x - 1000) >> 31); 
return 2 + ((999 - x) >> 31); 
return 2 + ((x + 2147482648) >> 31); 

An alternative for the fourth return statement is

return 8 + ((x + 1147483648) | x) >> 31; 

where the large constant is 2³¹ - 10⁹. This avoids both the and not and the signed shift.

Alternatives for the last if-else construction are

return ((int)(x - 1) >> 31) | ((unsigned)(9 - x) >> 31); 
return (x > 9) + (x > 0) - 1; 

either of which saves a branch.

If nlz(x) or ilog2(x) is available as an instruction, there are better and more interesting ways to compute ilog10(x). For example, the program in Figure 11-10 does it in two table lookups [CJS].

Figure 11-10 Integer log base 10 from log base 2, double table lookup.

int ilog10(unsigned x) {
   int y; 
   static unsigned char table1[33] = {9, 9, 9, 8, 8, 8, 
      7, 7, 7, 6, 6, 6, 6, 5, 5, 5, 4, 4, 4, 3, 3, 3, 3, 
      2, 2, 2, 1, 1, 1, 0, 0, 0, 0}; 
   static unsigned table2[10] = {1, 10, 100, 1000, 10000, 
      100000, 1000000, 10000000, 100000000, 1000000000}; 
 
   y = table1[nlz(x)]; 
   if (x < table2[y]) y = y - 1; 
   return y; 
} 

From table1 an approximation to ilog10(x) is obtained. The approximation is usually the correct value, but it is too high by 1 for x = 0 and for x in the range 8 to 9, 64 to 99, 512 to 999, 8192 to 9999, and so on. The second table gives the value below which the estimate must be corrected by subtracting 1.

This scheme uses a total of 73 bytes for tables, and can be coded in only six instructions on the IBM System/370 [CJS] (to achieve this, the values in table1 must be four times the values shown). It executes in about ten instructions on a RISC that has number of leading zeros but no other esoteric instructions. The other methods to be discussed are variants of this.

The first variation eliminates the conditional branch that results from the if statement. Actually, the program in Figure 11-10 can be coded free of branches if the machine has the set less than unsigned instruction, but the method to be described can be used on machines that have no unusual instructions (other than number of leading zeros).

The method is to replace the if statement with a subtraction followed by a shift right of 31 so that the sign bit can be subtracted from y. A difficulty occurs for large x (x 2³¹ + 10⁹) which can be fixed by adding an entry to table2, as shown in Figure 11-11.

Figure 11-11 Integer log base 10 from log base 2, double table lookup, branch-free.

int ilog10(unsigned x) {
   int y; 
   static unsigned char table1[33] = {10, 9, 9, 8, 8, 8, 
      7, 7, 7, 6, 6, 6, 6, 5, 5, 5, 4, 4, 4, 3, 3, 3, 3, 
      2, 2, 2, 1, 1, 1, 0, 0, 0, 0}; 
   static unsigned table2[11] = {1, 10, 100, 1000, 10000, 
      100000, 1000000, 10000000, 100000000, 1000000000, 
      0}; 
 
   y = table1[nlz(x)]; 
   y = y - ((x - table2[y]) >> 31); 
   return y; 
} 

This executes in about 11 instructions on a RISC that has number of leading zeros but is otherwise quite "basic." It can be modified to return the value 0, rather than -1, for x = 0 (which is preferable for the decimal conversion problem) by changing the last entry in table1 to 1 (that is, by changing "0, 0, 0, 0" to "0, 0, 0, 1").

The next variation replaces the first table lookup with a subtraction, a multiplication, and a shift. This seems likely to be possible because log₁₀x and log₂x are related by a multiplicative constant, namely log₁₀2 = 0.30103 .... Thus, it may be possible to compute ilog10(x) by computing for some suitable c 0.30103, and correcting the result by using a table such as table2 in Figure 11-11.

To pursue this, let log₁₀2 = c + e, where c > 0 is a rational approximation to log₁₀2 that is a convenient multiplier, and e > 0. Then for x 1,

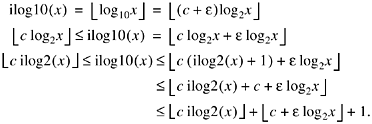
Thus, if we choose c so that c + elog₂x < 1, then approximates ilog10(x) with an error of 0 or +1. Furthermore, if we take ilog2(0) = ilog10(0) = -1, then (because 0 < c 1), so we need not be concerned about this case. (There are other definitions that would work here, such as ilog2(0) = ilog10(0) = 0).

Because e = log₁₀2 - c, we must choose c so that

This is satisfied for x = 1 (because c < 1) and 2. For larger x, we must have

The most stringent requirement on c occurs when x is large. For a 32-bit machine, x < 2³², so choosing

suffices. Because c < 0.30103 (because e > 0), c = 9/32 = 0.28125 is a convenient value. Experimentation reveals that coarser values such as 5/16 and 1/4 are not adequate.

This leads to the scheme illustrated in Figure 11-12, which estimates low and then corrects by adding 1. It executes in about 11 instructions on a RISC that has number of leading zeros, counting the multiply as one instruction.

Figure 11-12 Integer log base 10 from log base 2, one table lookup.

static unsigned table2[10] = {0, 9, 99, 999, 9999, 
  ?9999, 999999, 9999999, 99999999, 999999999}; 
 
y = (9*(31 - nlz(x))) >> 5; 
if (x > table2[y+1]) y = y + 1; 
return y; 

This can be made into a branch-free version, but again there is a difficulty with large x (x > 2³¹ + 10⁹) which can be fixed in either of two ways. One way is to use a different multiplier (19/64) and a slightly expanded table. The program is shown in Figure 11-13 (about 11 instructions on a RISC that has number of leading zeros, counting the multiply as one instruction).

Figure 11-13 Integer log base 10 from log base 2, one table lookup, branch-free.

int ilog10(unsigned x) {
   int y; 
  ?span
lang=EN-GB>static unsigned table2[11] = {0, 9, 99, 999, 9999, 
      99999, 999999, 9999999, 99999999, 999999999, 
      0xFFFFFFFF}; 
 
   y = (19*(31 - nlz(x))) >> 6; 
   y = y + ((table2[y+1] - x) >> 31); 
   return y; 
} 

The other "fix" is to or x into the result of the subtraction, to force the sign bit to be on for x 2³¹; that is, change the second executable line of Figure 11-12 to

y = y + (((table2[y+1] - x) | x) >> 31); 

This is the preferable program if multiplication by 19 is substantially more difficult than multiplication by 9 (as it is for a shift-and-add sequence).

For a 64-bit machine, choosing

suffices. The value 19/64 = 0.296875 is convenient, and experimentation reveals that no coarser value is adequate. The program is (branch-free version)

unsigned table2[20] = {0, 9, 99, 999, 9999, ..., 
  ?999999999999999999}; 
y = ((19*(63 - nlz(x)) >> 6; 
y = y + ((table2[y+1] - x) >> 63; 
return y;