15-2 Comparing Floating-Point Numbers Using Integer Operations

One of the features of the IEEE encodings is that non-NAN values are properly ordered if treated as signed magnitude integers.

To program a floating-point comparison using integer operations, it is necessary that the "unordered" result not be needed. In IEEE 754, the unordered result occurs when one or both comparands are NaNs. The methods below treat NaNs as if they were numbers greater in magnitude than infinity.

The comparisons are also much simpler if -0.0 may be treated as strictly less than +0.0 (which is not in accordance with IEEE 754). Assuming this is acceptable, the comparisons may be done as shown below, where and denote floating-point comparisons, and the symbol is used as a reminder that these formulas do not treat ?.0 quite right.

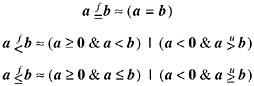
If -0.0 must be treated as equal to +0.0, there does not seem to be any very slick way to do it, but the following formulas, which follow more or less obviously from the above, are possibilities.

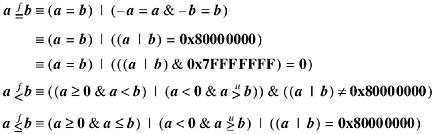
In some applications, it might be more efficient to first transform the numbers in some way, and then do a floating-point comparison with a single fixed-point comparison instruction. For example, in sorting n numbers, the transformation would be done only once to each number, whereas a comparison must be done at least times (in the minimax sense).

Table 15-2 gives four such transformations. For those in the left column, -0.0 compares equal to +0.0, and for those in the right column, -0.0 compares less than +0.0. In all cases, the sense of the comparison is not altered by the transformation. Variable n is signed, t is unsigned, and c may be either signed or unsigned.

The last row shows branch-free code that can be implemented on our basic RISC in four instructions for the left column, and three for the right column (these four or three instructions must be executed for each comparand).