15-3 The Distribution of Leading Digits

When IBM introduced the System/360 computer in 1964, numerical analysts were horrified at the loss of precision of single-precision arithmetic. The previous IBM computer line, the 704 - 709 - 7090 family, had a 36-bit word. For single-precision floating-point, the format consisted of a 9-bit sign and exponent field, followed by a 27-bit fraction in binary. The most significant fraction bit was explicitly included (in "normal" numbers), so quantities were represented with a precision of 27 bits.

Table 15-2. Preconditioning Floating-Point Numbers for Integer Comparisons
-0.0 = +0.0 (IEEE)	-0.0 < +0.0 (non-IEEE)
if (n >= 0) n = n+0x80000000; else n = -n; Use unsigned comparison.	if (n >= 0) n = n+0x80000000; else n = ~n; Use unsigned comparison.
c = 0x7FFFFFFF; if (n < 0) n = (n ^ c) + 1; Use signed comparison.	c = 0x7FFFFFFF; if (n < 0) n = n ^ c; Use signed comparison.
c = 0x80000000; if (n < 0) n = c - n; Use signed comparison.	c = 0x7FFFFFFF; if (n < 0) n = c - n; Use signed comparison.
t = n >> 31; n = (n ^ (t >> 1)) - t; Use signed comparison.	t = (unsigned) (n>>30) >> 1; n = n ^ t; Use signed comparison.

The S/360 has a 32-bit word. For single-precision, IBM chose to have an 8-bit sign and exponent field followed by a 24-bit fraction. This drop from 27 to 24 bits was bad enough, but it gets worse. To keep the exponent range large, a unit in the 7-bit exponent of the S/360 format represents a factor of 16. Thus, the fraction is in base 16, and this format came to be called "hexadecimal" floating-point. The leading digit can be any number from 1 to 15 (binary 0001 to 1111). Numbers with leading digit 1 have only 21 bits of precision (because of the three leading 0's), but they should constitute only 1/15 (6.7%) of all numbers.

No, it's worse than that! There was a flurry of activity to show, both analytically and empirically, that leading digits are not uniformly distributed. In hexadecimal floating-point, one would expect 25% of the numbers to have leading digit 1, and hence only 21 bits of precision.

Let us consider the distribution of leading digits in decimal. Suppose you have a large set of numbers with units, such as length, volume, mass, speed, and so on, expressed in "scientific" notation (e.g., 6.022 x 10²³). If the leading digit of a large number of such numbers has a well-defined distribution function, then it must be independent of the units—whether inches or centimeters, pounds or kilograms, and so on. Thus, if you multiply all the numbers in the set by any constant, the distribution of leading digits should be unchanged. For example, considering multiplying by 2, we conclude that the number of numbers with leading digit 1 (those from 1.0 to 1.999?times 10 to some power) must equal the number of numbers with leading digit 2 or 3 (those from 2.0 to 3.999?times 10 to some power), because it shouldn't matter if our unit of length is inches or half inches, or our unit of mass is kilograms or half kilograms, and so on.

Let f(x), for 1 x < 10, be the probability density function for the leading digits of the set of numbers with units. f(x) has the property that

is the proportion of numbers that have leading digits ranging from a to b. Referring to the figure below, for a small increment Dx, in x, f must satisfy

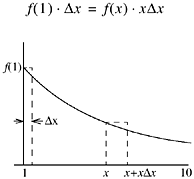
because f(1) ?Dx is, approximately, the proportion of numbers ranging from 1 to 1 + Dx (ignoring a multiplier of a power of 10), and f(x) ?xDx is the approximate proportion of numbers ranging from x to x + xDx. Because the latter set is the first set multiplied by x, their proportions must be equal. Thus, the probability density function is a simple inverse relationship,

Because the area under the curve from x = 1 to x = 10 must be 1 (all numbers have leading digits from 1.000?to 9.999?, it is easily shown that

The proportion of numbers with leading digits in the range a to b, with 1 a b < 10, is

Thus, in decimal, the proportion of numbers with leading digit 1 is log₁₀(2/1) 0.30103, and the proportion of numbers with leading digit 9 is log₁₀(10/9) 0.0458.

For base 16, the proportion of numbers with leading digits in the range a to b, with 1 a b < 16, is similarly derived to be log₁₆(b/a). Hence the proportion of numbers with leading digit 1 is log₁₆(2/1) = 1/log₂ 16 = 0.25.