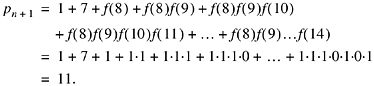16-2 Willans's Formulas

C. P. Willans gives the following formula for the nth prime [Will]:

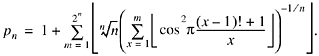
The derivation starts from Wilson's theorem, which states that p is prime or 1 if and only if (p - 1)! -1(mod p). Thus,

is an integer for x prime or x = 1 and is fractional for all composite x. Hence

Equation 1

Thus, if p(m) denotes ^[2] the number of primes m,

^[2] Our apologies for the two uses of p in close proximity, but it's standard notation and shouldn't cause any difficulty.

Equation 2

Observe that p(p_n) = n, and furthermore,

Therefore, the number of values of m from 1 to for which is p(m) < n is p_n - 1. That is,

Equation 3

where the summand is a "predicate expression" (0/1-valued).

Because we have a formula for p(m), Equation (3) constitutes a formula for the nth prime as a function of n. But it has two features that might be considered unacceptable: an infinite summation and the use of a "predicate expression," which is not in standard mathematical usage.

It has been proved that for n 1 there is at least one prime between n and 2n. Therefore, the number of primes 2ⁿ is at least n—that is, p(2ⁿ) n. Thus, the predicate p(m) < n is 0 for m 2ⁿ, so the upper limit of the summation above can be replaced with 2ⁿ.

Willans has a rather clever substitute for the predicate expression. Let

Then, if x < y, 1 y/(1 + x) y, so Furthermore, if x y, then 0 < y/(1 + x) < 1, so Applying the floor function, we have

That is, LT(x, y) is the predicate x < y (for x and y in the given ranges).

Substituting, Equation (3) can be written

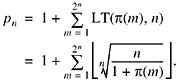
Further substituting Equation (2) for p(m) in terms of F(x), and Equation (1) for F(x), gives the formula shown at the beginning of this section.

Second Formula

Willans then gives another formula:

Here, F and p are the functions used in his first formula. Thus, mF(m) = m if m is prime or 1, and 0 otherwise. The third factor in the summand is the predicate p(m) =n. The summand is 0 except for one term, which is the nth prime. For example,

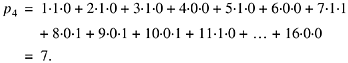
Third Formula

Willans goes on to present another formula for the nth prime that does not use any "nonanalytic" ^[3] functions such as floor and absolute value. He starts by noting that for x = 2, 3, ? the function

^[3] This is my terminology, not Willans's.

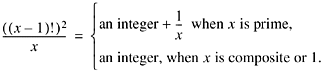
The first part follows from

and x divides (x - 1)! + 1, by Wilson's theorem. Thus, the predicate "x is prime," for x 2 is given by

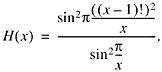
From this it follows that

This cannot be converted to a formula for p_n by the methods used in the first two formulas, because they use the floor function. Instead, Willans suggests the following formula ^[4] for the predicate x < y, for x, y 1:

^[4] We have slightly simplified his formula.

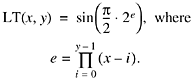
Thus, if x < y, e = x(x - 1)?0)(-1)?x - (y - 1)) = 0 so that LT(x, y) = sin(p/2) = 1. If x y, the product does not include 0, so e 1, so that LT(x, y) = sin((p/2) ?(an even number)) = 0.

Finally, as in the first of Willans's formulas,

Written out in full, this is the rather formidable

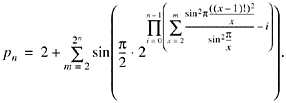
Fourth Formula

Willans then gives a formula for p_n+1 in terms of p_n:

where f(x) is the predicate "x is composite," for x 2; that is,

Alternatively, one could use f(x) = 1 - H(x), to keep the formula free of floor functions.

As an example of this formula, let p_n = 7. Then,