16-3 Wormell's Formula

C. P. Wormell [Wor] improves on Willans's formulas by avoiding both trigonometric functions and the floor function. Wormell's formula can in principle be evaluated by a simple computer program that uses only integer arithmetic. The derivation does not use Wilson's theorem. Wormell starts with, for x 2,

Thus, the number of primes m is given by

because the summand is the predicate "x is prime."

Observe that, for n 1, a 0,

Repeating a trick above, the predicate a < n is

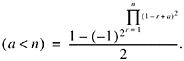
Because

we have, upon factoring constants out of summations,

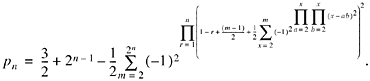
As promised, Wormell's formula does not use trigonometric functions. However, as he points out, if the powers of -1 were expanded using (-1)ⁿ = cospn, they would reappear.