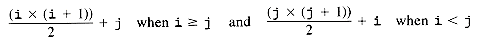Suppose a program involves an n ?/FONT> n array a that is always symmetric. In other words, it is initially symmetric, and any processing performed on a does not disturb its symmetry. When n is small, both the rowwise and columnwise representations are feasible, even though roughly one-half of the information being stored is superfluous. For large values of n (say, 400), the computer system may not provide the required 160,000 storage elements, so the program could not execute. One remedy may be to store only the diagonal entries of a and the entries below the diagonal (those whose row index i exceeds the column index j). This requires ((n ?/FONT> n) + n)/2 entries, or 80,200 instead of 160,000.
Although high-level languages could have provided a data-type, symmetric array to be used in this way, no language does. Instead, the programmer can construct a data array of length ((n ?/FONT> n) + n)/2 to store the entries. The idea is the same as for a rowwise representation, except that only those entries of a row in the lower half or on the diagonal of a are stored. Thus for the row in position i, entries a[i-1][0], a[i-1][1], . . . , a[i][i] are stored in consecutive entries of data, each row's entries following those of the preceding row. n
To use this representation of a, the programmer needs to be able to refer, for given i and j, to the proper position of data that corresponds to a[i][j], just as was done in the check function. Finding the offset formula is a little more complex than for the rowwise representation but is done in the same way.
Preceding the entries for the row in position i are the entries for rows in positions 0, 1, . . . , i - 1. The entry in position j of this row is then an additional j entries down in data. Thus the offset for a[i] [j] is 1 + 2 + 3 +. . . + i + j . Any reference we want to make to a[i] [j] is made, instead, by a reference to data [1 + 2 + ... + i + j]. This, of course, is true only for i ?/FONT> j, since a[i] [j], when i < j, is not stored in data directly. Its symmetric entry in a, a[j][i], is stored in data [1 + 2 + ... + j + i]. So if i < j, a reference to a[i] [j] must be achieved by referring to a[j] [i].
The polynomial (1 + 2 + . . . + i + j) (or ((1 + 2 + . . . + i) + j) appears at first glance to require a loop for its calculation, requiring time proportional to i. However,
The division is integer division, so the polynomial may be evaluated in constant time. This means that the entry in position (i,j) of a can be selected using the index,
Traversal may also be accomplished easily. Consider that the entries are stored in data for each row as records of variable length, yet they can be selected and traversed conveniently with no pointer array. The reason is that their lengths, and the order in which they are stored, are regular enough that the requisite calculations for positions can be made. In the general case of variable-length records, there is no way to do this.