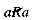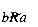You readily understand what is meant by the statements: "Fred is related to Sam"; "John is taller than Sue"; "3 is the square root of 9." The phrases each specify a connection or relation between two objects. In the first two cases the relations refer to two people. In the third case the relation refers to numbers. Each is a binary relation on a set of objects.
Mathematics abstracts from such examples to define a binary relation R on a set S. S is taken as the set or collection of objects referred to by the relation. R contains information, for any two of these objects, on whether or not they are related. R is a set of pairs of objects (a, b), where a and b belong to S. If the pair (a, b) belongs to R, then this is interpreted to mean that a is related to b. This is written as aRb. If (a, b) does not belong to R, then a is not related to b. This is written as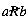 
.
For instance, specify S to be the set of integers between 2 and 10, so S = {2, 3, . . . , 10}; and take R = {(4, 2), (6, 2), (8, 2), (8, 4), (9, 3), (10, 2), (6, 3), (10, 5)}.Then R captures the "is divided evenly by but is not equal to" relation on S, since a pair (a, b) will belong to R only if a "is divided evenly by but is not equal to" b. By looking at R, we can determine if aRb or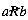 
for any a and b in S.
Of particular interest are the kinds of binary relations called partial orders. A binary relation R on S is called a partial order on S if it has the following properties:
n Irreflexivity For any a in S,
n Asymmetry For any two distinct a and b in S, aRb implies
n Transitivity For any three distinct a, b, and c in S, aRb and bRc implies aRc
These properties specify that whenever certain pairs are in R, then other pairs must necessarily be included in R or excluded from R. The "is divided evenly by but is not equal to" relation on S in the preceding paragraph fulfills all three properties of a partial order.
It is irreflexive, since a is divided evenly by but is equal to a for all a in S.
It is asymmetric, since if a "is divided evenly by" b, then b cannot be divided evenly by a when a is not equal to b.
It is transitive, since whenever a is divided evenly by b and b is divided evenly by c, then a must also be divided evenly by c.
To show that a relation does not have a property requires only one counter-example.
Two extreme binary relations on a set S are the null relation, which contains no pairs at all, and the universal relation, which contains all possible pairs. The null relation is a partial order. This is because no counterexamples can be found. The universal relation will never be irreflexive (unless S has no objects in it) or asymmetric (unless S has only one object), but it will always be transitive.
