primes(n)
1. Create a collection called candidates, consisting of all integers from 2 to n.
2. Remove all nonprime integers from candidates.
3. Print all integers that remain in candidates.
Consider first a simple function called primes.
primes(n)
int n;
{
collection candidates;
create(n,candidates);
remove(n,candidates);
print(n,candidates);
}
Primes may be obtained directly from the prime number algorithm when create, remove, and print are interpreted as functions carrying out steps 1, 2, and 3 of the algorithm, respectively. Note that no assumptions about candidates have been made. At this point it is of type collection, which has not yet been defined. Later in the process of developing the algorithm and program, collection, and thereby candidates, will be defined, after the basic operations on candidates become clear. Note that collection is a type, whereas candidates is a variable whose type must be declared. The next step is to refine and verify each function of primes. Refine means to express or define in more detail; verify means to confirm that a refinement does indeed do its job. To refine and verify create and print is straightforward enough, but to refine and verify remove is more difficult. If you want to know more about a state than you see in the first map of Figure 1.2, you may consult another map containing more information on the state's geography. Similarly, if you want to know how to carry out remove, a more detailed description may be available. If not, as is the case here, remove may be treated as a new problem whose solution must be found. One solution is this:
remove(n, candidates)
Set factor to the first prime.
While (nonprimes remain in candidates),
Delete from candidates all integers that are multiples of factor, and
Increase factor by 1.
It is again easy to see that, as long as each step is done correctly, the desired effect is obtained.
Still, more examination is needed to determine whether "nonprimes remain in candidates." It can be shown that nonprimes may remain in candidates only when factor is less than or equal to the square root of n. Consequently the condition (nonprimes remain in candidates) may be replaced by the condition
Delete is refined next (Figure 1.3). You should verify that this function correctly performs its task as long as omit takes nextmultiple out of candidates. It may help to simulate the execution of delete when n is 40 and factor is 2, and then 3.
Each task of function primes has now been defined and is, in fact, a complete C function. All other tasks, except for set, insert, belongs, and omit, have also been defined. Primes and all other tasks have been written modularly (functionally), meaning that for each task there is a function. For example, new functions have been introduced for each of the three tasks of primes: create, remove, and print. Had primes along with remove and delete not been functionally modularized, it would appear as follows:
This version is also a refinement of primes, but instead of defining new functions for its three tasks, the tasks have been replaced by program segments. Thus there are two basic ways to refine any task: (1) define a new function for the task, or (2) replace the task directly by its refinement expressed as a program segment in code. Compare this version with the functionally modularized form, the simple function primes given earlier. Notice that functional modularization suppresses detail.
Deciding how to modularize a program functionally is often a matter of individual taste, but as this text unfolds, the process will become clearer, and you will be able to develop your own style. Functional modularization is intended to highlight and isolate important tasks. The advantage of using functions may not be apparent with this simple prime number problem but will be striking in more complex problems.
Finally, the low-level tasks set, insert, omit, and belongs must be coded. To do this requires deciding how to implement candidates?/FONT>that is, deciding which data structures shall be used to store candidates and how to write the basic functions that operate on candidates. Recall that data structures such as candidates contain information and are operated on during the execution of a program. No matter how candidates is implemented, none of the functions already defined needs to be changed. They are independent of candidates implementation (except for the data declaration). As long as set, insert, omit, and belongs do their tasks correctly, no function invoking them needs to be changed. This is because we have written them treating candidates as a data abstraction. That is, we have assumed that candidates and the basic operations on it are available via functions (set, insert, omit, and belongs) and further, that any other operations on candidates have been expressed in terms of these functions. For instance, delete uses omit, and create uses insert. If, instead of calls to set, insert, omit, and belongs, the code defining them had been used, all functions containing these codes would be dependent on the implementation. Later, if we changed to a better implementation, it would be necessary to hunt through each function, find any code that would be affected by the change, and modify that code appropriately. A data abstraction consists of a data structure, to store data, and allowed operations on the data structure, to manipulate it. As a result, wherever one of these operations is invoked in a program, the data structure is being affected. Just as important, the data structure is not being affected unless one of these operations is invoked.
The use of data abstraction and functional modularization not only enhances understanding, but also simplifies maintaining a program. Maintenance is a crucial aspect of programming. It involves changing a program to do something new, to stop doing something, or to do better what it now does.
Using data abstractions as outlined above hides implementation details and makes the program independent of those details. On the other hand, the program's speed of execution and storage requirements will be greatly influenced by the implementation of the data abstraction. Consequently, the selection of an implementation should be based on the data abstraction's operations. Sometimes the choice that minimizes execution time and storage will be evident. More typically, conflicts arise, and the choice will involve trade-offs between time and storage. How to make this choice properly is a major focus of this text.
Consider two ways to implement candidates. It might be implemented as an integer array with the ith element of the array containing the value true if i is a prime and false if it is not. Alternatively, candidates could be implemented as an integer that is made up of contributions from each number in candidates. If the number i is in candidates, it contributes 2i. Thus if candidates consisted of 2, 3, 5, 7, and 9, its value would be 684(4 + 8 + 32 + 128 + 512). The integer is stored in an integer array of size one. Candidates could also be implemented as a dynamic list or tree and, indeed, one of these might be preferred. You might want to return to this problem after studying lists and trees, to verify that it can be converted to these structures. However, at this stage, arrays that are more familiar to you will be used. The code below defines the operations on candidates for the two array implementations. Each implementation should have its type declaration for collection global to primes and all its functions, as follows:
Note that the terms TRUE and FALSE are used in the boolean version. Since C does not have a type boolean, TRUE and FALSE must be defined before they are used in the program. In C, a true statement returns a non-zero value, and a false statement returns a zero. For consistency, write
TRUE and FALSE will be used for programming style in many places in the text. Programs that use them merely require the above statements. In the second version the function power (2,i) returns 2i.
Each implementation specifies a data structure for candidates and defines the same four basic operations allowed on it. Each entails some explicit restriction on the size of candidates. Such restrictions can be avoided by using the dynamic data structures introduced in later chapters.
The first implementation of candidates allows insert, omit, and belongs to be written so that they take constant time to execute. However, the amount of storage required will depend directly on n. The second implementation for candidates increases the execution times of the basic operations on candidates but reduces its storage requirement. In general, the choice of implementation for a data abstraction may be critical, determining whether a program will run to completion or abort because of insufficient time or storage. Section 1.8 discusses the selection of program and data structure in more detail. In any case, once the decision is made, the data declaration for candidates must appear in primes. The final result is a well-structured program. A complete program to run primes using the array implementation follows.
As noted, the first implementation for collection is used in the program. Notice that the declarations and definitions needed for the collection appear together in the program. Simply replacing that portion of the program with another implementation is all that is required to change to the new implementation. In Chapter 5 another way to package the collection and its operations for this program will be presented.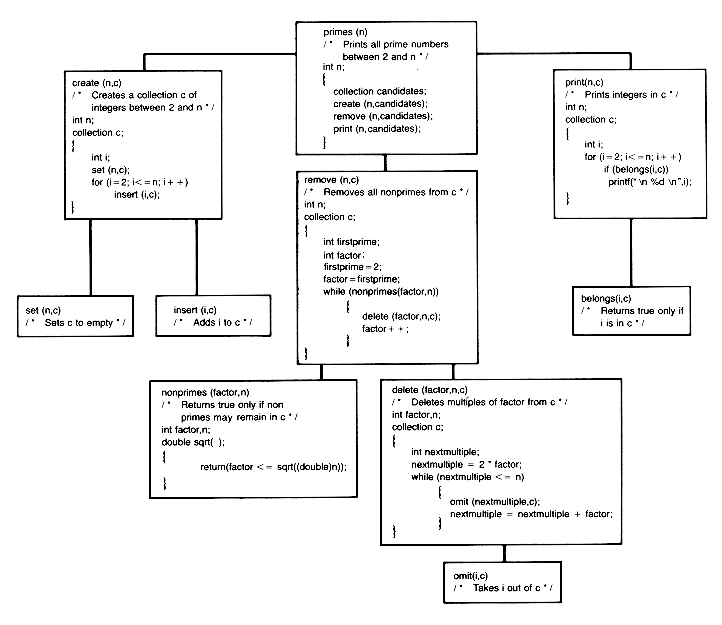
Figure 1.3 PRIMES Modularized
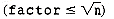. But doing this will make remove more difficult to understand. It is better to consider the evaluation of the condition as a new task that must be refined. We are now ready to write the function for remove and to verify it. The three functions appear in Figure 1.3, where set initializes the collection candidates to empty, insert adds the integer i to the collection, nonprimes is a function assumed to return the value true when 
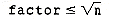and false otherwise, delete removes all integers from candidates that are multiples of factor, and belongs returns the value true if i is in candidates and false otherwise.primes(n)
int n;
{collection candidates;
int factor,i,nextmultiple;
int firstprime;
firstprime = 2;
double sqrt();
set(n,candidates);
for (i=2;i<=n;i++)
insert(i,candidates);
factor = firstprime;
while (factor <= sqrt((double)n))
{nextmultiple = 2 * factor;
while (nextmultiple <= n)
{omit(nextmultiple,candidates);
nextmultiple = nextmultiple + factor;
}
factor++
}
for (i=2;i<=n;i++)
if(belongs(i,candidates))
printf("\n %d\n",i);}
Candidates Implemented Candidates Implemented
as an Array as an Integer
typedef int collection[MAXN]; typedef int collection[1];
set(n,c) set(n,c)
/* Sets c to empty */ /* Sets c to empty */
int n; int n;
collection c; collection c;
{ { int i; c[0] = 0;
for (i=1;i<=n;i++) }
c[i] = FALSE;
}
insert(i,c) insert(i,c)
/* Inserts i into c */ /* Inserts i into c */
int i; int i;
collection c; collection c;
{ { c[i] = TRUE; int p,q;
} p = power(2,i);
q = (c[0]/p)%2;
c[0] = c[0] + (1-q)*p;
}
omit(i,c) omit(i,c)
/* Removes i from c */ /* Removes i from c */
int i; int i;
collection c; collection c;
{ { c[i] = FALSE; int p,q;
} p = power(2,i);
q = (c[0]/p)%2;
c[0] = c[0] - q*p;
}
belongs(i,c) belongs(i,c)
/* Returns true only /* Returns true ony
if i is in c if i is in c
*/ */
int i; int i;
collection c; collection c;
{ { return(c[i]); return((c[0]/power(2,i))%2);
} }
power (x,y)
/* Returns x to the power y */
int x,y;
{ int i,p;
p = 1;
for (i=1;i<=y;++i)
p = p*x;
return(p);
}
# define TRUE 1
# define FALSE 0
#include <stdio.h>
main()
{int n;
printf("\n n = ? \n");scanf("%d",&n);primes(n);
}
#define TRUE 1
#define FALSE 0
#define MAXN 500
typedef int collection[MAXN];
set(n,c)
/* Sets c to empty */
int n;
collection c;
{int i;
for (i=1;i<=n;i++)
c[i] = FALSE;
}
insert(i,c)
/* Inserts i in c */
int i;
collection c;
{c[i] = TRUE;
}
omit(i,c)
/* Removes i from c */
int i;
collection c;
{c[i] = FALSE;
}
belongs(i,c)
/* Returns true only
if i is in c
*/
int i;
collection c;
{return(c[i]);
}
primes(n)
/* Prints all prime numbers between 2 and n */
int n;
{collection candidates;
create(n,candidates);
remove(n,candidates);
print(n,candidates);
}
create(n,c)
/* Creates a collection of integers between 2 and n */
int n;
collection c;
{int i;
set(n,c);
for (i=2;i<=n;i++)
insert(i,c);
}
remove(n,c)
/* Removes all nonprimes from c */
int n;
collection c;
{int firstprime;
int factor;
firstprime = 2;
factor = firstprime;
while (nonprimes(factor,n))
{delete(factor,n,c);
factor++;
}
}
nonprimes(factor,n)
/* Returns true only if non
primes may remain in c
*/
int factor,n;
double sqrt();
{return(factor <= sqrt((double)n));
}
delete(factor,n,c)
/* Deletes multiples of factor from c */
int factor,n;
collection c;
{int nextmultiple;
nextmultiple = 2 * factor;
while (nextmultiple <= n)
{omit(nextmultiple,c);
nextmultiple = nextmultiple + factor;
}
}
print(n,c)
/* Prints integers in c */
int n;
collection c;
{int i;
for (i=2;i<=n;i++)
if (belongs(i,c))
printf("\n %d\n",i);}