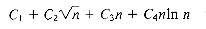For large n, this expression is dominated by the term C4n1n n. In fact, for large enough values of n, the expression will be no greater than C n1n n for an appropriate value of C. We describe this concisely by saying the expression is O(n1n n), read "order n1n n"; this notation will be used throughout the text.
By the storage requirements of primes is meant the total storage required for its data structures. Except for a few variables, the storage is required primarily for candidates and will be determined by its implementation. The analysis reveals that the bulk of the execution time for primes is spent executing the loop in delete. Consequently, to improve its time we speed up the time of the loop itself, or reduce the number of times it needs to be executed. For the array implementation, the storage required will be proportional to n, and this is where the bulk of the storage required is needed.
Primes can be improved in a number of obvious ways. Except for 2, no primes are even. Hence all other even numbers can be eliminated from consideration. This means that factor need never take on even values, so it can be increased by 2 instead of 1 in remove and can also be initialized to 3. Delete can be changed so that nextmultiple takes on only odd multiples of factor. With a little more work, candidates can be cut to roughly half its size by eliminating even integers. This will necessitate changes to set as well as changes to the for loops in create and print, but it reduces the storage needed by about one-half and the time by more than one-half.
Perhaps a less obvious improvement is to modify the increase of factor in remove so that, instead of increasing by 1 (or 2), factor increases to the value of the next prime in candidates (see Exercise 8). To realize this saving fully, it is necessary to use a new data structure, the list or the balanced binary tree, for the collection. Lists are discussed in Chapter 3, balanced binary trees in Chapters 7 and 9. These would save not only time but storage as well. Borrowing a result from mathematics about the distribution of prime numbers, we can state that any version of primes that stores all the primes from 2 to n in a collection will need n/ln n storage locations, since there are about that many such primes. Thus we will run out of storage before we run out of time!
Primes may be written so that its execution time increases but its storage needs decrease, or vice versa. Thus time is traded for storage, as is often done. Primes represents one extreme where all the primes are saved. A version of primes in which no primes are saved is at the other extreme (see Exercise 10). This version would require significantly more time.
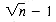 times, so the loop condition is evaluated
times, so the loop condition is evaluated 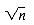 times. Assuming, for simplicity, that sqrt (n) takes constant time C, then
times. Assuming, for simplicity, that sqrt (n) takes constant time C, then 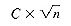 is the total time for the evaluation of the condition. If the loop task took constant time, then the total loop time would be the product of this constant and
is the total time for the evaluation of the condition. If the loop task took constant time, then the total loop time would be the product of this constant and 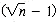 . Unfortunately delete's time varies, depending on the value of factor. Nonetheless, the total time for delete can still be derived.
. Unfortunately delete's time varies, depending on the value of factor. Nonetheless, the total time for delete can still be derived.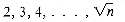 , the total number of delete's loop executions is
, the total number of delete's loop executions is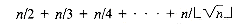
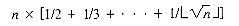
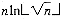 . The condition of this loop contributes roughly its own constant times
. The condition of this loop contributes roughly its own constant times 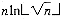 . The initialization of nextmultiple in delete contributes its constant times
. The initialization of nextmultiple in delete contributes its constant times 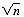 .
.