Consider the following declarations:
int book_number[80];
struct name author[40];
float prices[80];
char library[30];
The declaration specifies the name of each variable (e.g., book_number) and its type for each of four variables. It also specifies the range of values for an array index for each of the four arrays. An array index refers to a position of the array. Book_number,author,prices, and library have array indexes that may take on values in the range 0 to 79, 0 to 39, 0 to 79, and 0 to 29, respectively. In C the first position in an array is always the zero position. Book_number[3], author[9], and prices[5] refer to the fourth, tenth, and sixth entries, respectively, and library[12] refers to the thirteenth character in the character string library.
It has already been mentioned that arrays are very useful when entries must be accessed randomly. This occurs when the order in which requests for access to entries cannot be predicted. Suppose an array stores the initial mileage for each car of a fleet of rental cars. As a car is returned, its initial mileage is needed to prepare a bill based on mileage used. The next car to be returned can be any rented car. To access its initial mileage directly requires the random access capability of arrays. Processing time is saved, since the information entry is located directly?/FONT>no time is lost searching through other entries to find it. When information is accessed directly, in a constant time, it is said to be selected. Thus any array entry whose position is known can be selected.
Instead of accessing a single array entry, a programmer may wish to process an entire array by accessing and processing each entry in turn. Moving sequentially through the entries is a traverse. In this case, the program is said to traverse the array. Such a traversal would be required in order to print out, in order, the initial mileage of each car in the fleet. A complete traversal is accomplished when each entry has been processed exactly once. A simple loop, starting at the first entry and finishing at the last, will accomplish this. Another use of traversal is to find an array entry whose position is unknown. In this case, the loop is terminated when the entry is found. If the traversal is completed, it means the desired entry was not present.
Selection and traversal are two ways to access an array entry. If the entry's position is known, selection is the efficient way to access it. When successive array positions must be examined to find the entry, selection is not possible, but traversal may be used.
If the traversal terminates at the ith entry (because it is the desired one), then a time proportional to i is required, since the i - 1 preceding entries must be accessed before the ith entry is obtained. Selection, on the other hand, takes constant time. This is an important distinction between these two basic operations on arrays. Selection means you can go directly to what is wanted; traversal means you must rummage around to find it. Use selection when one or more accesses must be made in arbitrary order and traversal when each entry is to be accessed in sequence.
Example 2.1
Suppose that data, such as integers in the range 1 to 100, are stored in an array a, as shown in Figure 2.2. Given any valid index value in the variable i, print the number stored in the ith position of the array a. n
This may be done by executing the C statement
This is a concise, easy-to-understand solution to Example 2.1. It takes a constant amount of time to execute, since it selects the desired entry of a. Note that when the value of the index i is 7, then the array entry with the value 87 is printed; when the value of i is 5, then the entry with the value 3 is printed. The index i is avariable that points to a particular entry of a. The current value of the index i determines the entry currently selected. Changing the value of i changes the entry to which it points. Thus the solution can be interpreted as the command "Print the entry of a to which the index i currently points."
Example 2.2
Let a be an array of length n, and let k be a variable containing an integer in the range 1 to 100. If there is some value of i for which a[i] contains k, then print that value of i; if there is more than one such value, print any one of them. If the value of k is nowhere in a, then print "-1." n
Array a might represent the information kept by a car rental agency. For each i, array entry a[i] contains the account number, k, of the individual or firm currently renting car i. Example 2.1 thus requires finding the account now leasing car i. Example 2.2 requires finding the car being used by account k.
Example 2.2 could certainly be solved by traversing the array a, searching for an entry whose value equals the value of k. If one is found, its position in a would be printed. If the traversal is completed without success, "-l" would be printed. This solution is easy to code and could be written as follows:
Although this program segment for array traversal is simple, it is more complex than that for Example 2.1. Its execution time is proportional to the number of entries searched before the number in k is found, and if it is not found, the execution time is proportional to n.
Is it possible to find another way to solve this problem, one that will be as concise and clear as that for Example 2.1 and also execute in constant time? The answer is yes, if the information stored in a is represented in such a way that the program can select the correct value to print.
Such a program would start with creation of an array pointer of length 101, as follows. For each integer k (account number) between 1 and 100, if k does not appear in a, place "-1" in pointer[k]. If k does appear in a (it is an active account), place in pointer[k] the position of an entry of a that contains k. That is, place in pointer[k] the index value of an entry in a containing k. Thus, in Figure 2.3, pointer[3] contains 5, since a[5] contains 3.
With the array pointer available, the solution to Example 2.2 may be written as
This is the concise, easy-to-understand solution desired, and it executes in constant time. Again, the way in which the relevant information was represented in the program?/FONT>that is, the way in which the data was structured?/FONT>allows this solution to be achieved. Even in such a simple example, the way data is represented has a substantial impact on the resulting program.
Note that the use of the pointer array instead of a may cause some information available in a to be lost. This is because pointer captures only one of a's positions that contains a specific number, even though that number may appear in a more than once. Finally, a price in execution time must be paid to create pointer from a in the first place. However, if the solution to Example 2.2 needed to be executed repeatedly, for many values of k, then it probably would be worth the price. It is frequently the case that prior processing to extract or restructure data saves later processing time.
In terms of storage required, a takes up n storage entries, and pointer takes up 101 storage entries. If n is much larger than 101, then pointer even saves storage; if n is much smaller, it requires more storage. Thus it is possible to trade time for storage. It will become apparent that this is generally true: saving execution time requires more storage, and vice versa.
When the choice of data structure was the array a, Example 2.1 was solved using selection, but traversal was required to find a solution to Example 2.2. When the pointer array was chosen to represent information, selection could be used to solve Example 2.2 more efficiently. However, if we had wanted to know all the cars leased by account k, pointer would not have been sufficient. It would have been necessary to traverse a to find all the occurrences of account number k. Can you find a way to avoid this traversal?
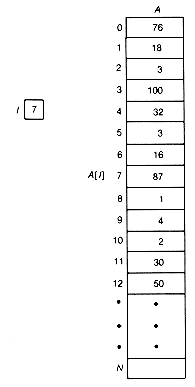
Figure 2.2 The Array for Example 2.1
printf("%d\n",a[i]);found = FALSE;
loc = 0;
while (found != TRUE && loc <= n)
if (a[loc] != k)
loc++;
else
found = TRUE;
if (found)
printf("\n %d\n",loc);else
printf("\n - 1 \n");printf("%d\n",pointer[k]);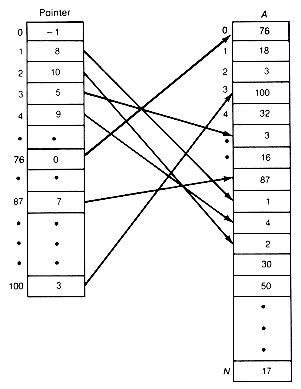
Figure 2.3 A Pointer Array for Example 2.2