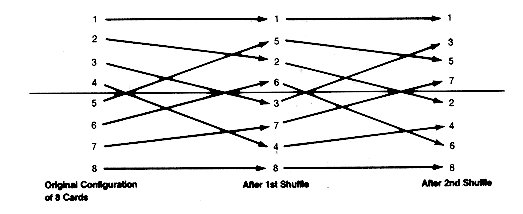
Using gambling terminology, a perfect shuffle of 2n cards occurs when the deck of cards is split into two halves and the shuffle interleafs the two halves perfectly. An original configuration of eight cards, with the configurations after two consecutive perfect shuffles, is shown in Figure 3.14 The cards are numbered one through eight. A third perfect shuffle would produce the original configuration.

Suppose a sequence of perfect shuffles is made for 2n cards. Eventually the original configuration must reappear. How many shuffles will it take before this happens? One way to find out is to execute code that performs such a sequence of shuffles, keeping track of how many are made, and printing this total when the original configuration occurs again. A program segment to do this can be written as follows:
initial(configuration,n);
numbershuffles = 1;
perfectshuffle (configuration,n);
while(!original(configuration,n))
{
perfectshuffle(configuration,n);
numbershuffles++;
}
Initial initializes configuration. Original returns true if configuration is the original, and false otherwise. Perfectshuffle changes configuration so that it reflects the new configuration resulting from a perfect shuffle. As written, this code is independent of how the configuration is actually implemented.