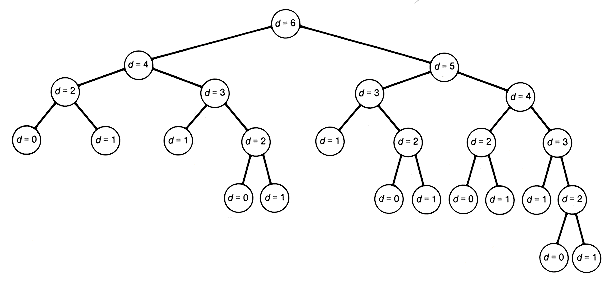
Consider the execution tree for these functions when d = 6, which is given in Figure 7.20. Each node of the tree represents a call to the recursive function Fibonaccitree. Nodes with the same d-value thus correspond to requests of the recursive function to carry out identical tasks, that is, to create identical trees.
Figure 7.20 shows a rather healthy-looking (nonsparse) tree with depth d = 6. This holds true for any value of d and means that while the storage is not excessive, the number of nodes in the tree will be O(fd), where f = (1 +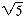 
)/2.* This is because
The execution tree for Fibonaccitree will always "resemble" the tree it is constructing.
The depth of an execution tree determines the size of the underlying stack needed for the program to execute properly.
The number of nodes in a Fibonacci tree of depth d is Fd+2 - 1.
Hence the execution time will increase exponentially with d. A close inspection reveals that many identical tasks or problems are solved repeatedly during its execution. For example, d = 0, 1, 2, 3, and 4 are solved 5, 8, 5, 3, and 2 times, respectively. This is what causes the excessive execution time and illustrates the situation to be wary of. When the same problems occur repeatedly, the efficiency can be increased if the algorithm can be modified to save the results for these problems so they may be used directly when needed instead of being regenerated by recursive calls. Of course, if this requires excessive storage, then such an approach won't do. Excessive storage is needed when an excessive number of distinct problems must be solved and their results saved. Still, this represents a viable strategy when applicable, as is the case here.
* In fact, the number of nodes will be 2Fd+1 - 1.
Notice that a Fibonacci tree of depth d ?/FONT> 2 can be constructed even if only Fibonacci trees of depth d - 2 and d - 1 are known. All that is necessary is to create a root node and append the tree of depth d - 2 as its left subtree and the tree of depth d - 1 as its right subtree. Consequently, the Fibonacci tree of depth d can be obtained by constructing the trees for depth 0, 1, 2 . . . , d in turn, while retaining only the lastest two. This gives the nonrecursive solution:
An Efficient Nonrecursive Version
If d = 0, then
set t to null;
else if d = 1, then
a. create a root node
b. set t to point to the root node;
else
c. set tl to null,
d. create a root node,
e. set tr to point to the root node, and
f. for k from 2 to d,
i. create a root node with tl its left subtree and tr its right subtree
ii. set t to point to the root node
iii. set tl to tr and tr to t.
This solution is efficient in both execution time and storage (see Exercises 16 and 17 of Chapter 4 for a related example).
Although it was possible to cut down drastically on the number of Fibonacci trees retained in this solution, such a saving not always possible. Sometimes solutions to all the problems generated by recursive calls will need to be retained. Even so, when this number is not excessive and an appropriate data structure can be found in which to store and efficiently access a solution when needed, then execution time can be improved. This is another instance of what we have frequently seen: time may be traded for storage.
It is hoped that you do not feel we have been barking up the wrong trees! Perhaps you even agree with the humorist Ogden Nash:
I think that I shall never see
A billboard lovely as a tree.
Indeed, unless the billboards fall
I'll never see a tree at all.