d = ?/FONT>lg2(n + 1)?/FONT>
This is important. Since the heaps dealt with initially in our heapsort algorithm are complete, their depth is O(lg (n)).
We now analyze the time required to create a heap by this algorithm. Starting from a complete binary tree is important. For instance, if we started with the binary tree shown in Figure 8.10, this algorithm would be equivalent to the original insertion sort of Section 8.3.4.
The heap creation algorithm does a total amount of work determined by the sum of the number of comparisons and interchanges needed in processing each node. A node at depth k cannot require more than k comparisons and k interchanges in its processing. The worst-case time will be achieved for any initial tree in which the numbers stored at nodes 1, 2, 3, . . . , n form an increasing sequence. For instance, if the integer i is stored at node i, for i = 1, 2, . . . , n, we obtain such an increasing sequence. If n is 15, the tree will be as shown in Figure 8.11.
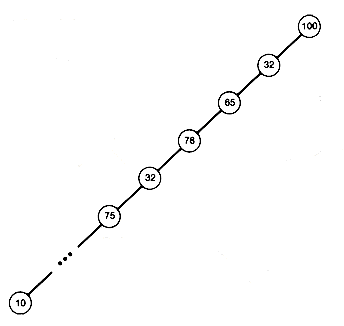
Figure 8.10 An Incomplete Binary Tree
It can be shown that the total time for such a tree to be turned into a heap by the algorithm is proportional to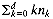 
, where n is the number of nodes at depth k, d is the depth, and k is the number of comparisons and interchanges required for each node at depth k. This is because every record will work its way to the root of the tree when it is processed. Since nk = 2k-1, this sum will be proportional to n lg n. The efficiency of this method can be increased somewhat by first determining where a record to be processed will end up along its path to the root, and then shifting everything down before inserting it. This efficiency could also have been achieved with the insertion sort.
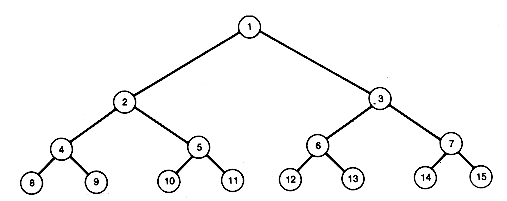
Figure 8.11 Binary Tree with Numbers Forming an Increasing Sequence