In Chapter 7, three important traversals through the nodes of any binary tree were defined: 1) preorder, 2) inorder, and 3) postorder. In order to search a binary tree to determine if a particular key value is stored, any one of those traversals could be used to gain access to each node in turn, and the node tested to see if the search key value is there. This would be equivalent to a linear search.
Instead, the special nature of binary search trees facilitates highly efficient search. We simply compare the search key with the root key. If they match, the search is complete. If not, determine whether the search key is smaller than the key at the root. If so, then if it is in the tree at all, it must be in the left subtree. If it is larger than the root key, it must be in the right subtree if it is in the tree at all. Thus either the left or right subtree is eliminated from consideration. This procedure is repeated for the subtree not eliminated. Eventually, the procedure finds the key in the tree or comes to a null subtree and concludes that the key is not stored in the tree.

Assume that nodes of the binary search tree are represented as follows.
typedef struct treenode
{
whatever info;
struct treenode *leftptr;
struct treenode *rightptr;
}binarytreenode, *binarytreepointer;
This special search may be implemented as follows:
found = FALSE;
p = t;
pred = NULL;
while ((p != NULL) && (!found))
if (keyvalue == p->key)
found = TRUE;
else if (keyvalue < p->key)
{
pred = p;
p = p->leftptr;
}
else
{
pred = p;
p = p->rightptr:
}
Found indicates whether the search key value was present in the tree. If so, p points to the node in which the search key was found, and pred points to its predecessor. If the search key was not found, then pred points to the node that would have been its predecessor had it been in the tree. Note that this allows additional information to be obtained, if desired, beyond the fact that the search key was not found. The key less than the search key and the key greater than the search key can easily be determined, so that records closest to the desired one are known.
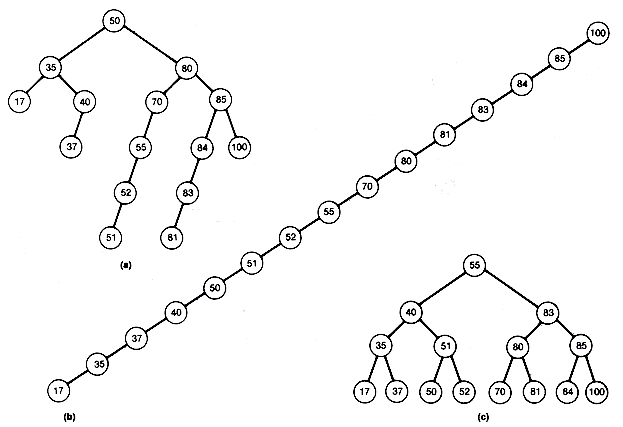
Notice that when (b) of Figure 9.7 is searched in this way, the search is equivalent to a linear search of an array in which the records are stored in sorted order. This search algorithm, applied to (c), would be equivalent to a binary search of an array in which the records are stored in sorted order. A search of (a) would fall somewhere between these two extremes.
What allows the search of Figure 9.7(c) to be equivalent to a binary search? It is the fact that the tree is "scrunched up" or near minimum possible depth, and not as straggly (unnecessarily deep) as the others. It has an intuitive kind of "balance," so that we eliminate from consideration about half the records each time we make a comparison. We are back to the game of "twenty questions.''