One difficulty remains. How can the programmer be certain the algorithm can actually be carried out? It may be impossible to carry out because at some point there may be no objects with zero predecessors. That this is indeed an algorithm requires showing that there always is at least one object with no predecessors.
One method of proof for any proposition is to assume it is not true and then show that this assumption leads to a contradiction. This method of proof is applied here. The goal is to prove that every time the loop task is to be carried out, at least one object with no predecessors can be found among those remaining. To assume that this is not true means that at some point the task cannot be carried out because every object left has at least one predecessor. Recall that the original diagram, representing a partial order, had no loops. It will be shown that the assumption implies a loop in the diagram. This will be the contradiction.
Suppose i1 is one of the remaining objects. Under the assumption, every object has at least one predecessor, so i1 has a predecessor (say, i2). Note that i2 cannot be the same object as i1, or the irreflexivity property would not hold. Again, i2 must have a predecessor (say, i3). The object i3 cannot be i1 or i2. If it were i1 or i2, then a loop involving i2 and i1 or a loop with just i2 would exist. Continuing with this argument, i1, i2, i3, i4, . . . must all be distinct objects. But since there are only n objects in total, eventually an object must repeat. This implies that the repeated object is the starting and ending object of a loop. The conclusion is that the assumption was false. Therefore what we wanted to prove must be true, and we never get bogged down?/FONT>there will always be an object with no predecessors.
This algorithm yields additional insight into the topological sorting problem. Since it is clear that the loop can always be carried out to completion, it will always produce a topological sort of the n objects. In other words, a topological sort always exists. This was certainly not obvious before.
To be sure the algorithm is understood, it is applied next to Example 11.6, depicted again in Figure 11.3. Initially (see Figure 11.3(a)), 4, 7, 5, and 9 have zero predecessors.
The first step is to select and remove 5 (either 4, 7, or 9 could also have been removed) and its successor arrows, to obtain Figure 11.3(b). S is not empty, so the loop must be repeated. Now, 4, 7, and 9 have no predecessors. Select and remove 7 and its successor arrows, and obtain Figure 11.3(c). S is still not empty, and now 4, 9, 1, 3, and 6 have no predecessors. Select 4. Updating produces Figure 11.3(d).
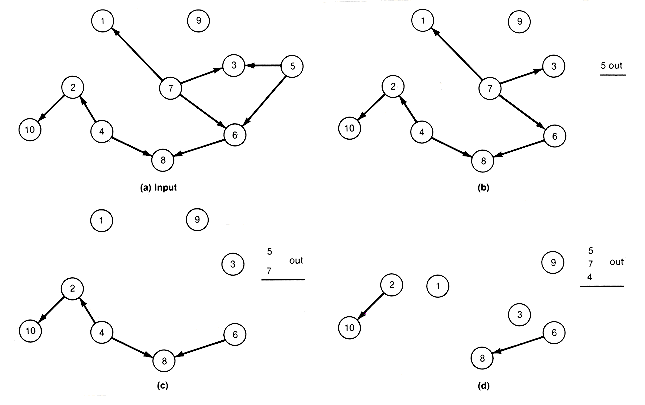
S is still not empty, but 9, 1, 3, 6, and 2 now have zero predecessors. Continuing in this way, removing 1, 3, 6, 8, 9, 2, and finally 10 in succeeding iterations yields the final ranking: 5, 7, 4, 1, 3, 6, 8, 9, 2, 10.
Notice that every time an object is selected and removed, the diagram is updated to reflect the new S and the new partial order. As a result, some additional objects may end up with zero predecessors. Once an object has zero predecessors, it will remain in each succeeding diagram, always with zero predecessors, until it is removed.
The first refinement describes an implementation of the algorithm.
First refinement:
1. Read n.
2. Initialize for phase I.
3. While there is another input pair,
a. record the information in the pair i, j phase I
4. Initialize for phase II. phase II
5. While the set S is not empty,
a. select an object with no predecessors, and output it as the next object in the output ranking;
b. update the records to reflect the removal of the output objects.
Phase I reads into memory the information about the number of objects and the partial order. Every time an i, j pair is read in, the new information that this represents must be incorporated into a representation in memory. The "record the information" of task 3a refers to the modification of this representation to reflect the new arrow, i ?/FONT> j.
Phase II describes the processing required by our algorithm. Task 5a involves the selection, removal, and outputting of an object. Task 5b involves modifying the partial order representation and S, to reflect the removal of an object and its arrows, and outputting it in the ranking. After task 5b is carried out, that representation should reflect the new set S and the new partial order resulting from the object's removal.
