Assume the weights are w1, w2, . . . , wn and are indexed so that w1 ?/FONT> w2 ?/FONT> . . . ?/FONT> wn. You should convince yourself that an optimal binary tree must be a full binary tree.* An optimal tree can always be found, since the number of full binary trees with n terminal nodes is finite. It is clear that the Huffman construction yields optimal trees for n = 1 and 2. This is the basis for the induction, which will be on the number of weights or terminal nodes, n. The induction hypothesis is that the Huffman construction yields optimal trees for any n - 1 weights. We must show that as a result, it must generate optimal trees for n weights.
*See Exercise 5.
Given any tree with n terminal nodes, Tn, in which Figure 12.8(a) appears as a subtree, let T?/FONT>n - 1 be the tree with n - 1 terminal nodes obtained from Tn by replacing this subtree by the terminal node shown in Figure 12.8(b). Then the weighted path length of Tn equals the weighted path length of T?/FONT>n - 1 + (w1 + w2).
Given T?/FONT>n-1, inversely, Tn can be obtained from it. Therefore, Tn must be optimal with respect to weights w1, w2 . . . , wn, if and only if T?/FONT>n-1 is optimal with respect to weights (w1 + w2), w3, . . . , wn. This is because if only one tree were not optimal, it could be replaced by an optimal tree, thus improving the weighted path length of the corresponding version of the other.
By the induction hypothesis, the Huffman construction yields a tree, T?/FONT>n-1, with n - 1 terminal nodes, that is optimal with respect to weights (w1 + w2), w3, . . . , wn. The corresponding tree, Tn, with n terminal nodes, is just the tree given by the Huffman construction for weights w1, w2 , . . . , wn . Since T?/FONT>n-1 is optimal, so is Tn. This completes the proof.
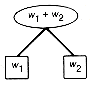
(a) Subtree
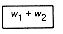
(b)Terminal Node after Combining Weights
Figure 12.8 Subtree Replacement