Consider the tree of Figure 13.14. In the link-inversion traversal, for every descent to the left from node.p (that is, every traversal of the left subtree of node.p), the left pointer field of node.p was set to point to node.p's predecessor. For every descent to the right (to traverse the right subtree of node.p), the leftpointer of node.p was restored to its original value, the tag of node.p was set to 1, and the right pointer field of node.p was set to point to node.p's predecessor. Consequently, having completed the traversal of the left subtree of some node q, it was possible to follow the backward pointing pointers to get to q. Q was the first node encountered with a tag value of 0, on the path back.
The Robson traversal does not have tag fields available for this purpose. Instead, a stack is kept in the tree itself, which will allow node q to be found. Q is the root of the most recent subtree, whose nonnull left subtree has already been traversed and whose nonnull right subtree is in the process of being traversed. A variable top is used, and kept updated, to point to the current node q. A variable stack is used, and kept updated, to point to the next most recent subtree whose nonnull left subtree has already been traversed and whose nonnull right subtree is in the process of being traversed. Variables p and predp are used, as in link inversion, to point to the node currently being processed and to its predecessor, respectively. Each stack entry, except the current top entry, is kept in the "rightmost" terminal node of one of the subtrees whose nonnull left subtree has been completely traversed, and whose nonnull right subtree is in the process of being traversed. In Figure 13.14, when node.p is being processed, there are four subtrees whose left subtrees have already been traversed and whose right subtrees are currently being traversed. Their roots are labeled 1 to 4 in Figure 13.14. Nodes 1, 3, and 4 have nonnull left subtrees. Each of these nodes has its left pointer field pointing to its predecessor and its right pointer pointing to the root of its left subtree. Node 2, which has a null left subtree, has its original null value, and its right pointer field is pointing to its predecessor. Nodes 1, 3, and 4 are thus the roots that must have stack entries. Top points to the most recent, node 1. Stack points to the stack entry corresponding to the next most recent root, node 3. This stack entry is kept in the rightmost terminal node of node 1's left subtree. This rightmost node has its left pointer field pointing to the node that contains the next stack entry, and its right pointer field pointing to its corresponding root (node 3 in this case). All stack entries (except the first, pointed to by top) have this same format. In Figure 13.14, the last stack entry points to node 4.
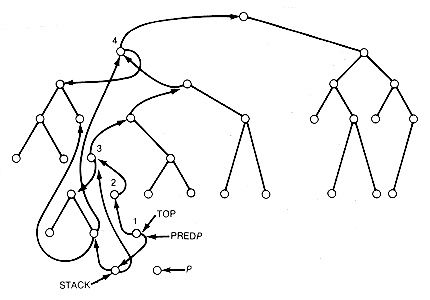
Figure 13.14 Robson Traversal Configuration of the Binary Tree T
Notice that a path back to the root always exists from node.predp. In Figure 13.14, after node.p is processed, the traversal of node 1's right subtree has been completed. This also completes the traversal of the right subtrees of nodes 2 and 3 and the left subtree of node 3's predecessor. The Robson traversal now proceeds by following the backward path, restoring appropriate left or right subtrees along the way, until the predecessor of node 3 is encountered. At this point, its right subtree must be traversed. Figure 13.15 shows the situation just before that traversal . During the traversal of the backward path, if node.predp has a null right subtree, or top=predp, then we are coming from the left subtree of node.predp, otherwise from the right subtree. Thus the stack entries allow node q to be found even though no tag fields are used.
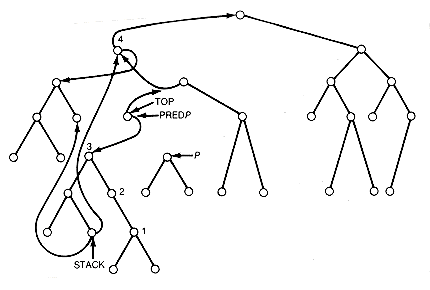
Figure 13.15 Robson Traversal before P Is Processed in the Binary Tree T
During the backtracking, the stack is popped, and top is updated as necesssary. Top and stack are initialized to null, predp to null, and p to t. An additional variable avail is used and updated to point to a terminal node every time one is encountered, so that its pointer fields are available if a new stack entry must be created. In this case, the available node must retain a pointer to node.top in its right pointer field and a pointer to the current entry to which stack points in its left pointer field; stack must be updated to point to the new entry; and top must be updated to point to the new top root. At all times, the path from predp back to the root is stored in the tree, as well as the stack of entries pointing to roots of subtrees (with nonnull left subtrees), whose left subtree traversals have completed, and whose right subtrees are being traversed. Each node along the path from predp to the root is in one of the following states:
If the node's left subtree is being traversed, then
its left pointer is pointing to its predecessor, and its right pointer is undisturbed.
If the node's right subtree is being traversed, then
if the node has a null left subtree, then
its right pointer is pointing to its predecessor
else
its left pointer is pointing to its predecessor, and its right pointer is pointing to
the root of the node's left subtree.
The following routines are to be used with the preorder traversal so that it implements the Robson traversal. Stack is declared to be of the same type as binarytreepointer, and s plays the role of predp.
Routine Task
-----------------------------------------------------------------------------
setnull( ) determined by the implementation
setstack(&s) sets top, stack, and s to null
push(p,&s) if leftptr.p is not null then
set leftptr.p to s and s to p
else
set rightptr.p to s and s to p
left(p) returns a copy of leftptr.p
right(p) returns a copy of rightptr.p
nextsubtree(&s, &p) set avail to p
set found to false
while((not found) and (s not null))
if top = s, then
save stack in hold, pop the stack by setting
top to rightptr.stack, stack to leftptr.
stack, and leftptr.hold and
rightptr.hold to null. Save leftptr.s in
pred, restore leftptr.s by setting it to
rightptr.s, restore rightptr.s by setting it
to p, set p to s, and s to pred
else
if leftptr.s = null, then
save rightptr.s in pred, restore
rightptr.s by setting it to p, set p to s,
and s to pred
else
if rightptr.s null, then
push an entry for s onto the stack by
setting leftptr.avail to stack,
rightptr.avail to top, stack to
avail, and top to s. Return the value
of rightptr.s, set rightptr.s to p,
and set found to true
else
save leftptr.s in pred, restore
leftptr.s by setting it to p, set p to s,
and s to pred.
if s = null, then
return null.